方差是衡量随机变量或一组数据离散程度的度量,用来度量随机变量和其数学期望(即均值)之间的偏离程度。在Excel 2016中,我们有两个计算方差的函数,分别是VAR.P函数和VAR.S函数。
VAR.P函数计算的是基于整个样本总体的方差。其基本语法包括一个必需参数,即总体的第一个数值参数,以及可选的2至254个数值参数。计算公式如下:
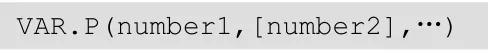
图:方差计算公式
VAR.S函数则用于估算基于样本的方差。其参数和VAR.P类似,但基于样本而不是总体。计算公式如下:

图:样本方差计算公式
公式中的x_bar为样本平均值,n为样本大小。
示例15-43 产品包装质量比较
假设有甲、乙、丙3个车间包装产品,每个产品的目标重量为100g/袋。现在对3个车间各随机抽取10袋产品进行称重,称重数据如图15-49所示。
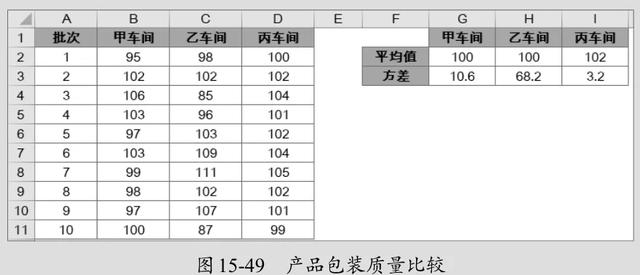
图:产品称重数据
在G2单元格中输入以下公式,并向右复制到I2单元格,计算各车间包装产品的平均重量:
=AVERAGE(B2:B11)
在G3单元格中输入以下公式,并向右复制到I3单元格,计算各车间包装产品的偏离程度:
=VAR.P(B2:B11)
通过对比可以看出,甲、乙车间平均质量均为100g,丙车间超出100g,所以丙车间包装质量较差。
甲车间方差为10.6,乙车间方差为68.2,二者相比,甲车间的方差较小,说明包装质量更加稳定。
使用STDEV.P函数和STDEV.S函数计算标准差
标准差在概率统计中常用来测量统计分布程度,反映组内个体之间的离散程度。即使两组数据的平均值相同,它们的标准差也可能不同。在Excel 2016中,我们有两个计算标准差的函数,分别是STDEV.P函数和STDEV.S函数。标准差是方差的算术平方根,二者关系如下:
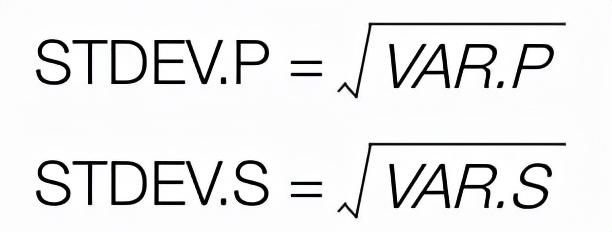
图:标准差与方差的关系
STDEV.P函数计算基于整个样本总体的标准偏差,基本语法包括一个必需参数,即总体的第一个数值参数,以及可选的2至254个数值参数。计算公式如下:

图:STDEV.P函数计算公式
STDEV.S函数基于样本估算标准偏差,其参数和VAR.S类似。计算公式如下:
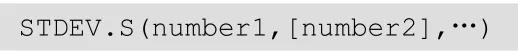
图:STDEV.S函数计算公式
公式中的x_bar为样本平均值,n为样本大小。
示例15-44 某班学生身高分布
在图15-50中,A~B列是某班学生身高记录表的部分内容。在E1单元格中输入以下公式计算得到学生的平均身高,结果为177.33(cm):
=AVERAGE(B2:B41)
在E2单元格中输入以下公式,计算学生身高的标准差,返回结果为7.30:
=STDEV.P(B2:B41)
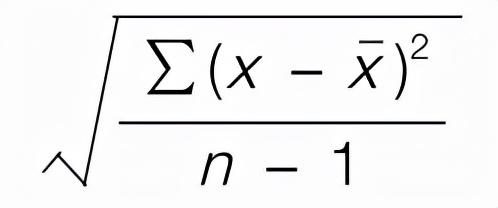
图:学生身高分布
由此可以说明,此班学生的身高主要分布在177.33 ±7.30cm之间。













